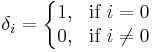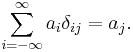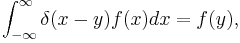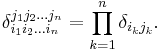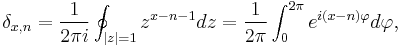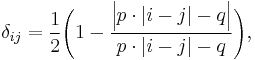Kronecker delta
In mathematics, the Kronecker delta or Kronecker's delta, named after Leopold Kronecker (1823-1891), is a function of two variables, usually integers, which is 1 if they are equal, and 0 otherwise. So, for example,
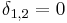 , but
, but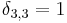
It is written as the symbol δij, and treated as a notational shorthand rather than as a function.
Contents |
Alternate notation
Using the Iverson bracket:
Often, the notation 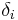 is used.
is used.
In linear algebra, it can be thought of as a tensor, and is written 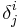 .
.
Digital signal processing

Similarly, in digital signal processing, the same concept is represented as a function on  (the integers):
(the integers):
![\delta[n] = \begin{cases} 1, & n = 0 \\ 0, & n \ne 0.\end{cases}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4414b458f7fe5bb968ab94a466b0d6dc.png)
The function is referred to as an impulse, or unit impulse. And when it stimulates a signal processing element, the output is called the impulse response of the element.
Properties of the delta function
The Kronecker delta has the so-called sifting property that for 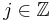 :
:
and if the integers are viewed as a measure space, endowed with the counting measure, then this property coincides with the defining property of the Dirac delta function
and in fact Dirac's delta was named after the Kronecker delta because of this analogous property. In signal processing it is usually the context (discrete or continuous time) that distinguishes the Kronecker and Dirac "functions". And by convention,  generally indicates continuous time (Dirac), whereas arguments like i, j, k, l, m, and n are usually reserved for discrete time (Kronecker). Another common practice is to represent discrete sequences with square brackets; thus:
generally indicates continuous time (Dirac), whereas arguments like i, j, k, l, m, and n are usually reserved for discrete time (Kronecker). Another common practice is to represent discrete sequences with square brackets; thus: ![\delta[n]\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2b63622fadf95b2200b264909054224f.png) . It is important to note that the Kronecker delta is not the result of sampling the Dirac delta function.
. It is important to note that the Kronecker delta is not the result of sampling the Dirac delta function.
The Kronecker delta is used in many areas of mathematics.
Linear algebra
In linear algebra, the identity matrix can be written as 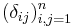 .
.
If it is considered as a tensor, the Kronecker tensor, it can be written 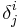 with a covariant index j and contravariant index i.
with a covariant index j and contravariant index i.
This (1,1) tensor represents:
- The identity matrix, considered as a linear mapping
- The trace
- The inner product
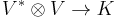
- The map
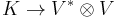 , representing scalar multiplication as a sum of outer products
, representing scalar multiplication as a sum of outer products
Extensions of the delta function
In the same fashion, we may define an analogous, multi-dimensional function of many variables
This function takes the value 1 if and only if all the upper indices match the corresponding lower ones, and the value zero otherwise.
Integral representations
For any integer n, using a standard residue calculation we can write an integral representation for the Kronecker delta as the integral below, where the contour of the integral goes counterclockwise around zero. This representation is also equivalent to a definite integral by a rotation in the complex plane.
Algebraic representation
If  and
and  are decimal numbers with no more than
are decimal numbers with no more than 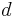 decimal digits, the Kronecker delta function can be represented by means of the following algebraic expression:
decimal digits, the Kronecker delta function can be represented by means of the following algebraic expression:
where  and
and 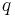 are arbitrary integers that satisfy
are arbitrary integers that satisfy 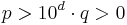 .
.
For instance, if  and
and  are integers, the simplest choice is:
are integers, the simplest choice is: 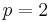 ,
, 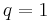 . On the other hand, if
. On the other hand, if  and
and  belong to a set of decimal numbers with
belong to a set of decimal numbers with 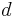 decimal digits, the simplest choice is:
decimal digits, the simplest choice is: 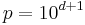 ,
, 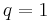 .
.
See also
- Levi-Civita symbol –
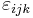
- Dirac measure
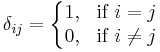
![\delta_{ij} = [i=j ].\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b17d8699b618ec6e77e5d14234f9cdb3.png)